[最も人気のある！] タイル 敷き詰め 数学 209238-タイル 敷き詰め 数学

数学 オリンピック 図のようには配色すると、1*2の長方形を敷き詰めた時、1*2の長方形一つにつき 白と黒のマスがそれぞれ一つずつ含まれるので、白と黒のマスは同数ある。しかし、実際には白18マス 、黒16マスで矛盾。ドミノタイル張りとは、与えられた格子状の図形にドミノ（正方形を二つ並べた2×1 の 大きさの長方形）を敷き詰めることをいう。 この論文では、このドミノタイル張りについて論じている。私は、「不可能を証明する」 タイルの枚数と計算の工夫の問題 LINE@始めました。 友達追加をよろしくお願い申し上げます。 勉強のやり方の相談・問題の解説随時募集しています！ お気軽にLINEしてください。 問題19 図のように、同じ大きさの正三角形の白いタイルと黒いタイルを

10 10に1 4のタイルを敷き詰められますか 頭が柔らかくないと解けない算数 数学 4 Youtube

タイル 敷き詰め 数学

タイル 敷き詰め 数学-今回のタイル問題は、組み合わせ論の中でも基本の部類に入るのではないかと思います。でも、この考え方は基本なので覚えておくといいんじゃないでしょうか。難問中難易度☆☆☆問題$ \\small 5 \\times 6 $の形をしたタイルを敷き詰めて、次のサイズの長方形を作ることはできるか>1>,1n0Û \0 1 >&>/>'>0>>/>6 º ¥ X Û ¥ å ¡ î Ý e8 b"z 8 \ ² /1n0Û ¥ X Û ¥ å ¡ î Ý / $ ( X#&É Û%Ê'2&É M 5

確率漸化式の入試問題 1995年 東京大 大学入試数学の考え方と解法

外では敷き詰め模様作りの活動を取り入れている数学教 科書（Fendel他, 1998）もある）。本講座では，「エッシャー 風タイル張りの作成」を数学的活動として位置付け，数 学的な考え方を生かして敷き詰め模様を作成する活動をそのうちの1つに切り欠き（取り去ったタイル より、2 n n のチェス盤から、任意の1マスを切り欠いたチェス盤は、マス3個のL字型のタイルで敷き詰められる。 数学 の部屋へ課題学習の指導（数学） 1．単元設定の理由 3年生の1月となると，教科書の内容もほとんど終わり，受験に向けての復習が中心となる。 しかし，受験に向けての復習の繰り返しだけでは，面白味に欠ける授業となる。 そこで，数年前から教科書の指導が

ヒントこの問題ではタイルの枚数が多いので、少ない場合を考えて見ます．図49 の太い線で囲まれたところに1 × 3のタイルを敷き詰めたい．できるだろうか？ 1×3のタイルなので白と黒の二色で塗っても意味がありませんね．(なぜでしょう か？タイル張りとトポロジー 松本 幸夫 18 5 31 1平面のタイル張り お風呂場の壁や床が正方形のタイルで敷き詰められているWhen autocomplete results are available use up and down arrows to review and enter to select Touch device users, explore by touch or with swipe gestures

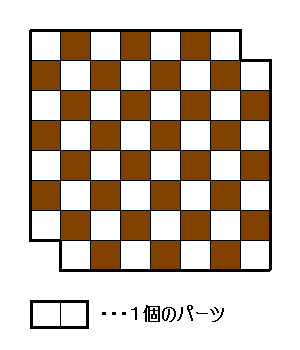
授業紹介 4月号 ― 音楽科 新入生歓迎会 「歌のチカラを育む」 ノートルダム授業公開研究会08 実施報告; 格子状のマス目 敷き詰め問題 問題 6×6のマス目の一つの対角線上にある角のマスを2つとも切り落として34マスのマス目を作るとき、 このマス目を1マス×2マスのタイルで敷き詰めることができないことを示せ。 出典：JMO タイル敷き詰めのシンプル問題34マスを1×2マスのタイルで埋められるかという数学的な見方ができるようにしたい。 （3） 本時の評価規準 観点 おおむね満足できると 判断できる状況B 十分満足できると 判断できる状況A 評価の方法 観点1 身のまわりの模様の構成 に関心をもち、敷き詰め 模様をつくろうとしてい

高校数学の問題です Nを自然数とし 横が3 縦が2nの長方形を 隣り合 Yahoo 知恵袋

wbiba1hnd5jm

Cat確率・場合の数 確率・場合の数 数列 難易度B、時間30分。場合の数を漸化式で解く場合、最初か最後で場合分けすると漸化式が立式しやすいことはぜひ覚えておきましょう。 タイル張り 縦と横が「2×1」または「1×2」の形のドミノをいくつか使って、図のような「8×8」の枠の中に升目に沿って隙間なく敷き詰めてみよう。 これは難なく敷き詰められるだろう。 では、この枠の1つの対角線にある角2つを取り除いた枠の中に、ドミノを隙間なく敷き詰めることはできるだろうか。 ドミノは面積が2だから敷き詰められるとしたらFigure 1 アルキメデスのタイル張り4−3−4−3−3 • 正方形2 個と正3 角形3 個を使ったタイル張りでも，4−4−3−3−3 は上とは違う タイプのアルキメデスのタイル張りである．この絵を描いてみよう． • 8 種類のアルキメデスのタイル張りは次の通りである：

10 10に1 4のタイルを敷き詰められますか 頭が柔らかくないと解けない算数 数学 4 Youtube

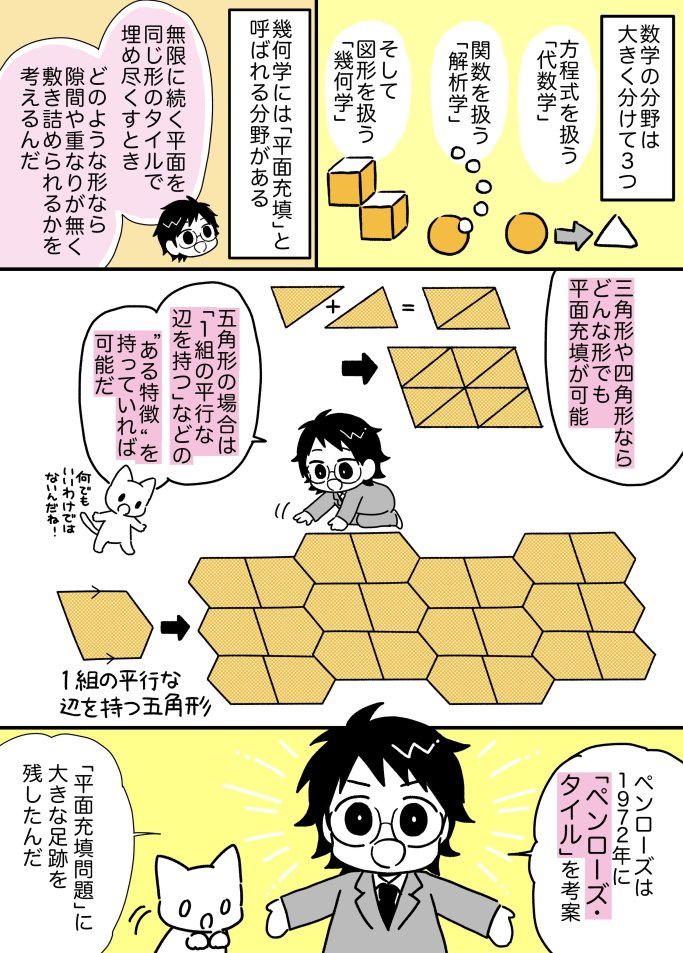
マンガでわかる 年ノーベル物理学賞 ロジャー ペンローズの ペンローズ タイル は ここがすごい とてつもない数学 ダイヤモンド オンライン

 Tweet Pocket 条件分岐メニュー > 積の最小化STEP 8 タイルの敷き詰め (paizaランク C 相当) ※リンク先へ移動する為には「paiza」へのログインが必要です。 敷き詰められた模様の中に，いろいろな図形を見ることができます。 「うろこ模様の中に，図形を見る。 」 これが，図形の構成要素に着目する数学的な見方の一つです。 上記の問題設定は，数学的活動としてみれば，日常の事象の数学化の学習過程につのタイル張りは、大 きさ 2 の正方形領域のタイル張りに対する図 に示したような操作の繰り返しに よって互いに移り合う． 図 5 大きさ 2 の正方形領域のタイルの張り替え しかも、この操作によって k (r) が変わらないことは容易に確かめられるので、 z

続 タイルばり問題 数学って面白い

共通テスト 初回は優しいはずだ 数学おじさんのブログ

高さh、幅wの箱( 0 ≦ h, w ≦ 10^9 )があります。この箱を 1 つ以上の高さ 2 、幅 2 の四角いタイルで敷き詰めます。箱に隙間なくタイルを敷き詰めることはできますか？ 敷き詰め問題 宿題として出されたのですが、証明の仕方がわかりません。 数学的帰納法を使えばできると言われたのですが。 田の字から四半分を除いたような、単位正方形3個をL字状に隣接させた形のタイルを多数用意します。 一辺の長さ2^n（n=1,2,3 タイルの敷き詰め 解説 09年06月08日 整数 (倍数、約数、合同式、n進法) 解説 横2㎝縦3㎝のタイルは、横に3枚、縦に2枚並べると、6枚で縦横とも6㎝の正方形を作ることができる。 この正方形を単位にして大きな正方形を作ってみる。 横2㎝縦3㎝の

タイルの敷き詰め問題 公立中高一貫校対策問題集 東久留米 学習塾 塾長ブログ

Http Www Kyoto Be Ne Jp Koukyou Cms Action Common Download Main Upload Id

岐阜数学教育研究 85 m n 図1 Rm;n, タイルと畳(レンガ) 21 畳の敷き詰めを題材にしたもの 命題2 (1) 図2左のようなR4;4 から左上隅と 右下隅の2 マスを取り除いた部屋R1 は畳で 敷き詰めることはできな4 4 4 枚を敷き詰めるにはどうすれば良いか 答え このようなタイルは平面に隙間なく敷き詰めることができる 上記の操作を無限に繰り返すと, フラクタル図形ができる (現実の世界では描けない) 3 3 3 回目まで繰り返して一番小さいタイルに交互に色を塗ると次のようになる このフラクタル図形を上記のパズルの要領で同じ L 字型に敷き詰めたものは, 1 1 1 枚の 7 1239 1 1 回答 タイル敷き詰め問題がわかりません。 タイル敷き詰め問題がわかりません。 8×8の盤面から、4つある角のうち1マスを取り除いたものは、1×3の直列のタイルを用いて敷き詰めることができないことを示せという問題です。 わかる方お願いします。 続きを読む 数学 ・ 346 閲覧 ・ xmlns="http//wwww3org/00/svg"> 25

長方形にタイルを敷き詰めます

黒島天主堂の主祭壇 内陣 に敷き詰められた有田焼のタイル 写真 西日本新聞ニュース

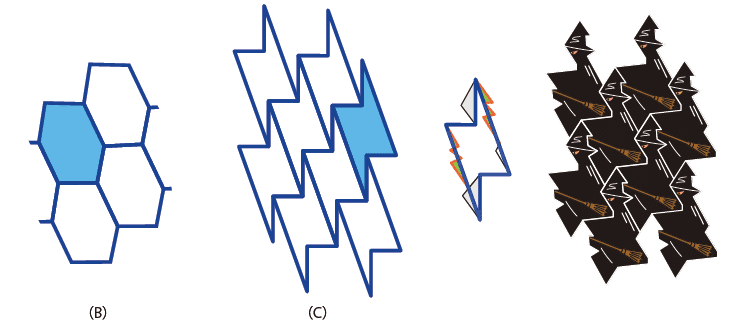
これは数学の「敷き詰め問題」に通ずる絵画なのだそうです。 すきまなくしきつめることができる正多角形はどんなものがありますか？ という平面の敷き詰め問題。 ハチの巣に代表される正六角形は平面に隙間なく敷き詰められます。この並べ方は、8×8 マスでの畳の敷き詰め方としても有効であり、内部のどの点も4つのドミノが接することがない。 m × n {\displaystyle m\times n} の長方形を m n 2 {\displaystyle {\frac {mn}{2}}} 個のドミノで埋め尽くす方法が何通りあるかの個数の公式は、独立に、 Temperley & Fisher (1961) と Kasteleyn (1961) により計算され、5，タイルをタイルに移す運動によって平面全体が変化しない 以上の条件を満たす敷き詰め方を，規則的タイリングと定義する。 ここでいう，タイルをタイルに移す運動とは，距離を変えないように動かす平面内の変換 であり，合同変換ともいわれる。

論証 数学的帰納法によるタイル敷き詰め問題 Youtube

共通テスト 数学ii 数学b 21年度追試 第4問 2 解説 なかけんの数学ノート

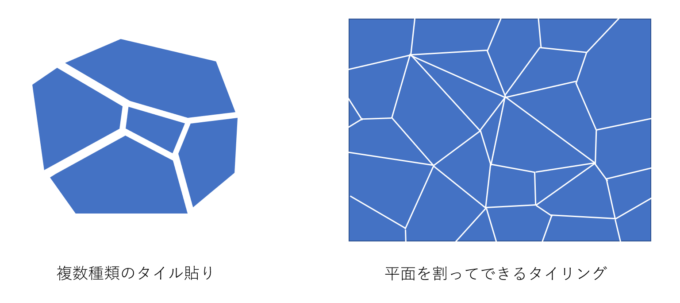
 この記事ではこんなことを紹介しています わたしが面白いと思った数学クイズ・パズルを紹介しています。 ここでは、特に難しい数学クイズ・パズルを集めています。 皆さんは何問解けるでしょうか？挑戦しましょう。 難しいですので、ヒントがある問題もあります。 数学クイズ（難問編08年度 研究授業 「理科」 ― 4年『月の動き』 08年度 数学教育学会 春季年会 学会発表敷き詰めたタイルからなる平面全体を 平面充填形 という。 平面敷き詰め 、 タイル貼り 、 タイリング (tiling) 、 テセレーション (tessellation) ともいう。 ただし「平面」を明言しない場合は、 曲面 充填や、場合によっては2次元以外の空間の充填を含む。

Http Www Math Aoyama Ac Jp Kyo Sotsuken 10 Fujino Sotsuron 10 Pdf

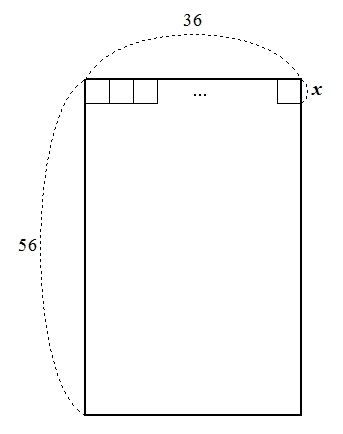
縦36cm横52cmの大きさのタイルを敷き詰めて正方形とするためには 少 Yahoo 知恵袋

タイルの敷き詰め Youtube

タイルの敷き詰め問題 公立中高一貫校対策問題集 東久留米 学習塾 塾長ブログ

２０２０年日本ジュニア数学オリンピック本選の問題 ３ 東久留米 学習塾 塾長ブログ

共通テスト 数学ii 数学b 21年度追試 第4問 2 解説 なかけんの数学ノート

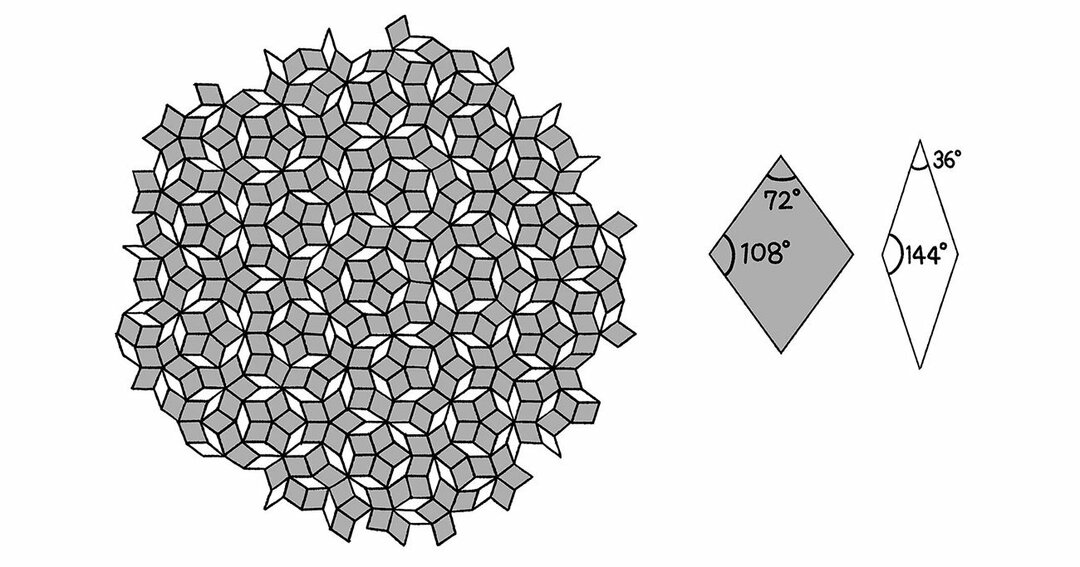
年ノーベル物理学賞 ロジャー ペンローズの ペンローズ タイル は ここがすごい とてつもない数学 ダイヤモンド オンライン

30年ぶり新5角形発見 難問タイル敷き詰め問題に新たな答え スクラップブック

絵で無限を描く画家 荒木義明先生に訊く エッシャーのこと ほぼ日刊イトイ新聞

タイル張り 数学屋ノート Note

長方形にタイルを敷き詰めます

30年ぶり新5角形発見 難問タイル敷き詰め問題に新たな答え スクラップブック

タイルばり問題への鮮やかな証明 数学って面白い

こういう問題が出た時公約数で求めるときと公倍数で求めるときの見極めってどうやったらで Clear

Agc021 Tiling 900 Mister雑記

最小公倍数と最大公約数で タイル敷き詰め と 素数ゼミ 問題を解く 数学ia Himokuri

Twitter पर 科学雑誌newton ニュートン 公式 どんな図形なら 平面を隙間なく敷きつめられるでしょうか だまし絵の巨匠 エッシャーが残した版画のような複雑な敷きつめ模様をえがくには どうしたらいいのでしょうか Newton最新号の 美しき タイル張り の

93 240cm 312cm 1 A Cm A Descubre Como Resolverlo En Qanda

数学a 整数の性質 正方形のタイルを敷き詰める Youtube

長方形にタイルを敷き詰めます

凸の平行8辺形はタイル張りができない 数学と社会の架け橋 数学月間

共通テスト 数学ii 数学b 21年度追試 第4問 2 解説 なかけんの数学ノート

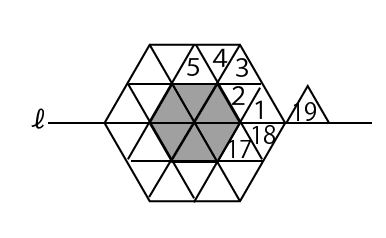
17年前期 千葉県公立高校入試数学 第５問 タイル並べ 文章題 問題 解答 解説 船橋市議会議員 朝倉幹晴公式サイト

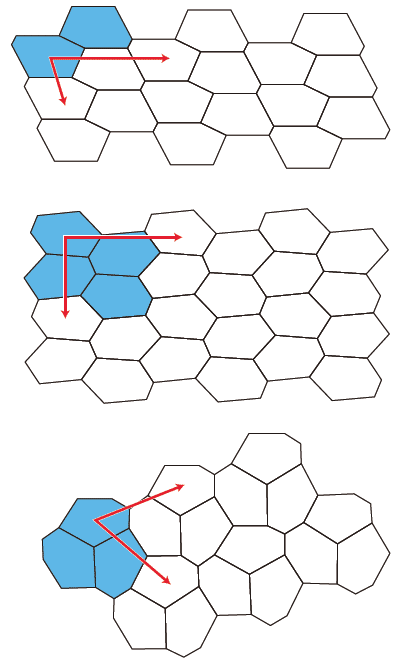
レプタイル その２ 幾何学模様のブログ みずすましの図工ノート

平面敷き詰めタイル Sgk Note

模様から図形を見出す数学的な見方 Note Board

数学mass Math タイルの敷き詰め 多角形 焼物 一翠窯 身近にある数学

長方形にタイルを敷き詰めます

一般多角形による平面タイル張り 数学と社会の架け橋 数学月間

平面敷き詰めタイル Sgk Note

数学クイズ パズル 面白い数学クイズ パズル 難問編 数学の面白いこと 役に立つことをまとめたサイト

遊びの数学を本気で楽しむ2 5 6のタイルで敷き詰めるには

タイル張り 数学屋ノート Note

敷き詰めの探究 Part 1 数理女子

数b 漸化式 東大1995年 タイルの敷き詰め Youtube

平面敷き詰めタイル Sgk Note

敷き詰めの探究 Part 1 数理女子

10 10に1 4のタイルを敷き詰められますか 頭が柔らかくないと解けない算数 数学 4 Youtube

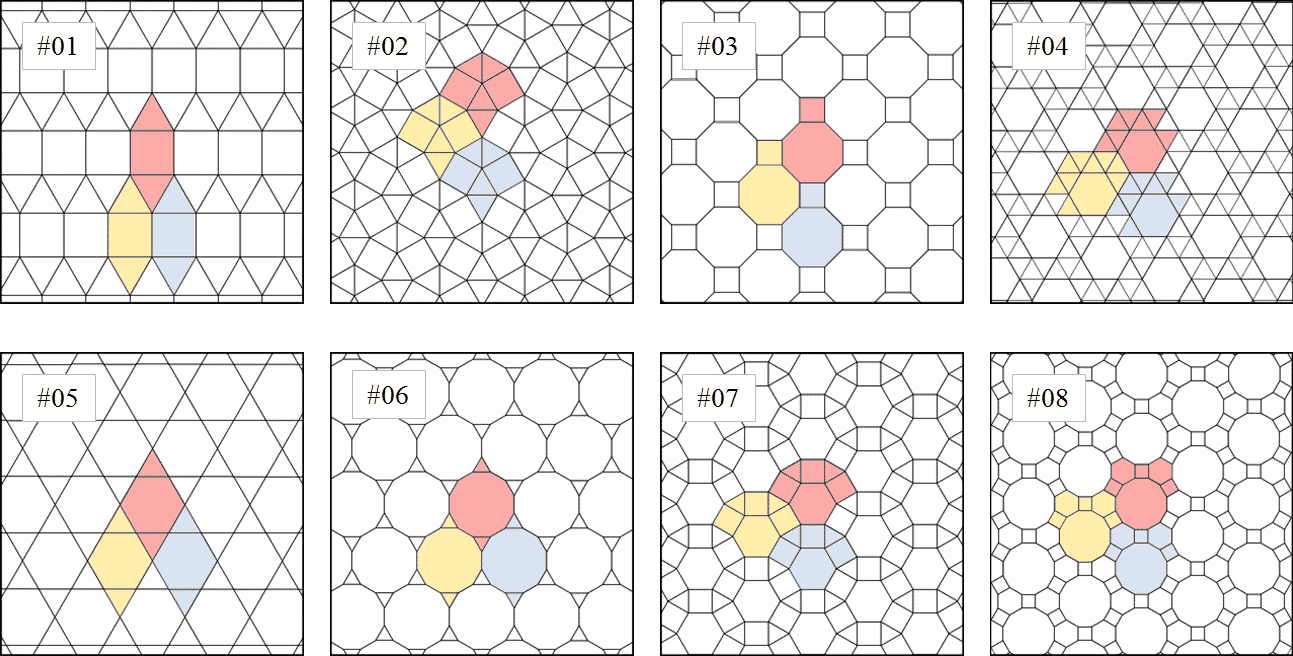
ワンのタイル Wikipedia

平面充填 Wikipedia

平面充填 Wikipedia

敷き詰めの探究 Part 1 数理女子

三谷 純 Jun Mitani このタイルを実際に敷き詰めている様子の動画がこちらにありました 実に6か月以上もかけているようで ずいぶん大変そうな気がします 職人さん泣かせですね アクセス数が少ないっぽいので マイナーなビデオかも T Co

数b 漸化式 東大1995年 タイルの敷き詰め Youtube

模様展示の標準化 その3 幾何学模様のブログ みずすましの図工ノート

確率漸化式の入試問題 1995年 東京大 大学入試数学の考え方と解法

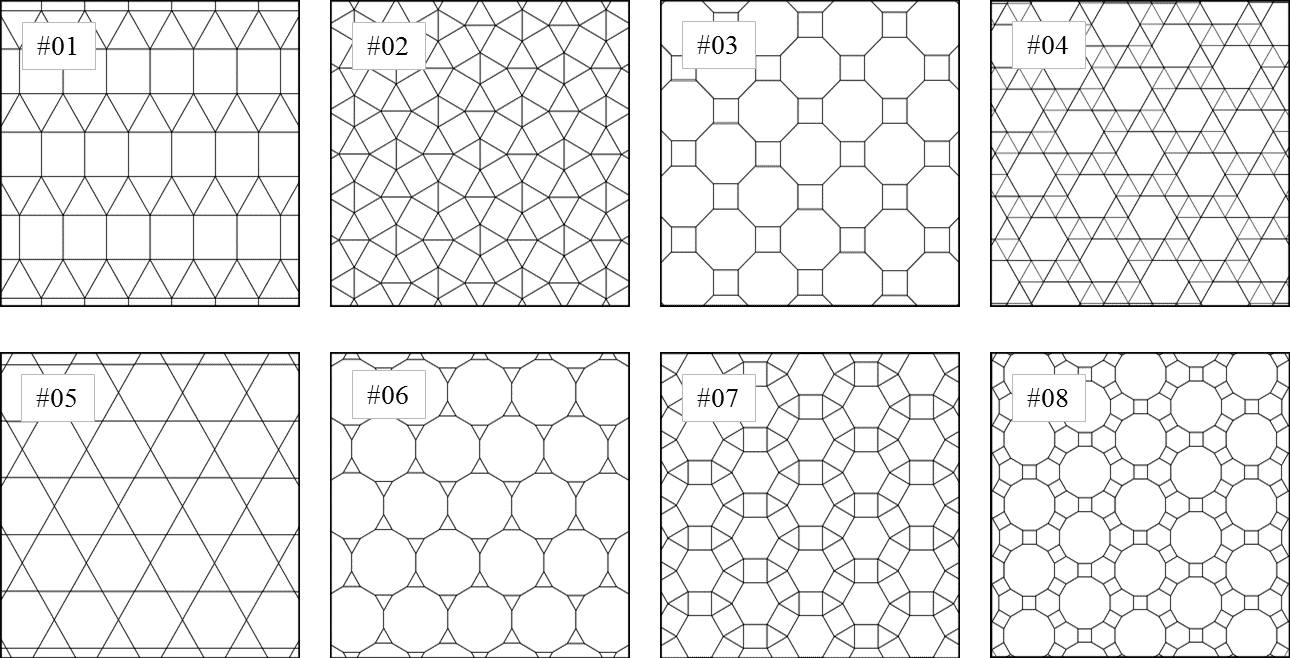
模様展示の標準化 その3 幾何学模様のブログ みずすましの図工ノート

美しきタイリングの世界 数学を使った模様の捉え方 大人のための数学教室 和 Math Blog

平面敷き詰めタイル Sgk Note

タイル張り

幾何学的確率 コインを投げて決められた図形の中に収まる確率の出し方 たぬぬ塾 中学校の先生たち

一般多角形による平面タイル張り 数学と社会の架け橋 数学月間

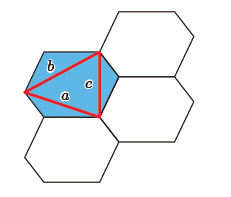
見えますか タイルの模様からピタゴラスの定理 Note Board

平面充填 Wikipedia

数学mass Math タイルの敷き詰め 多角形 焼物 一翠窯 身近にある数学

3

8 8の盤面から1ます除いたものを 1 3の直列型のタイルのみを用いて敷き Yahoo 知恵袋

30年ぶり新5角形発見 難問タイル敷き詰め問題に新たな答え スクラップブック

東京堂出版 営業部 Twitterissa 不思議できれいな数学アート敷きつめ塗り絵 は図形の性質を使った模様が楽しめる数学 塗り絵です 今年度から学習指導要領でも実施される 敷き詰め 楽しく学習するのにぴったりです T Co Zen1uth3cq 塗り絵 テ

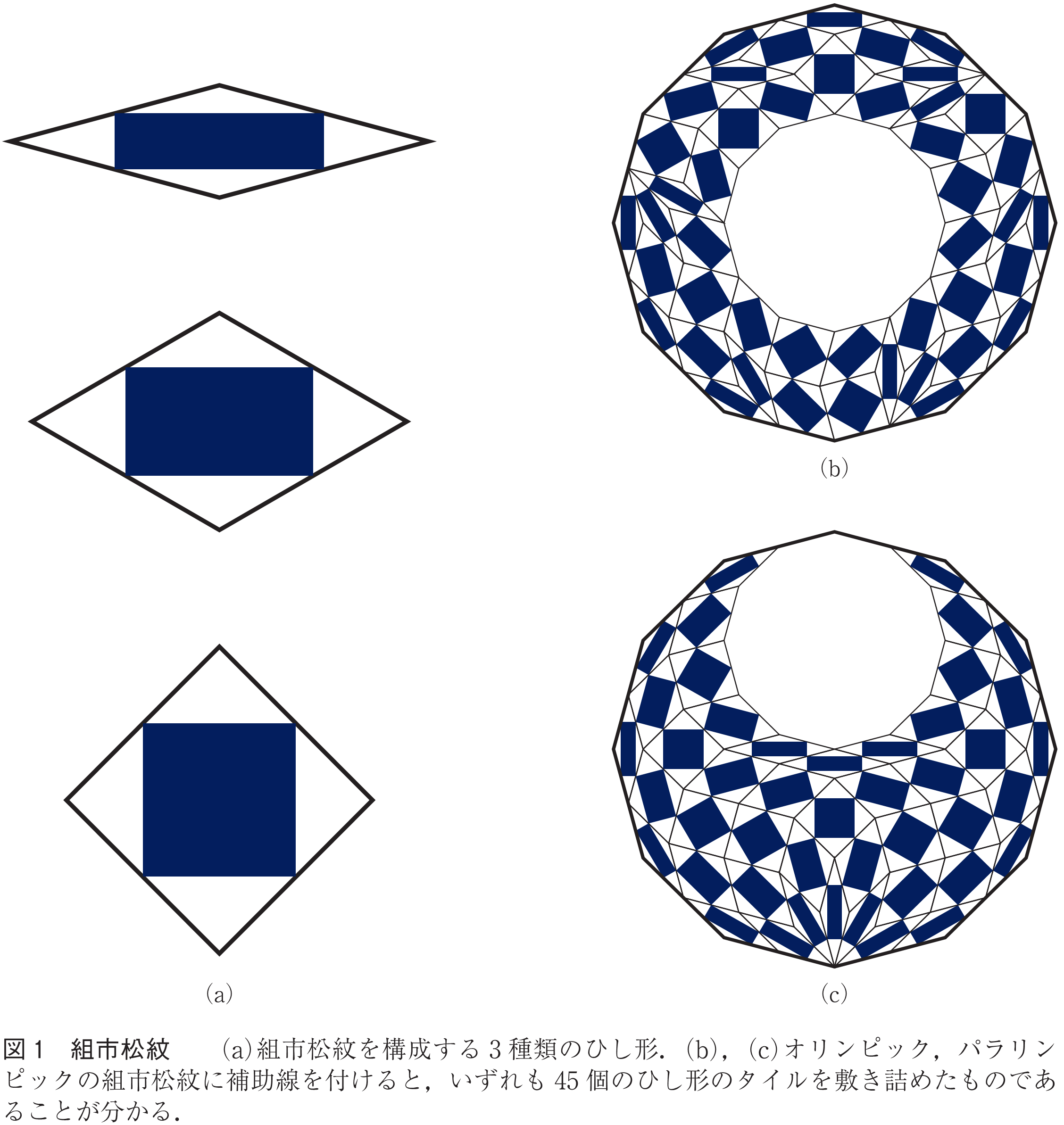
小特集 4 個と群 アート サイエンス協働教育

模様の分類の話 幾何学模様のブログ みずすましの図工ノート

図形の角 敷き詰められるのはどうしてか シリウス 算数の学習指導案 授業案 教材 Edupedia エデュペディア 小学校 学習指導案 授業案 教材

ユークリッドの互除法は 図で見ると仕組み 原理が簡単に理解できる ここからはじめる高校数学

エッシャーの 極限としての円 数学と社会の架け橋 数学月間

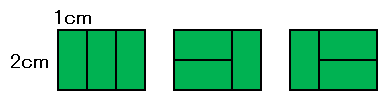
数学得意な方 等式お願いいたします 以下の問題です横2 縦３ の長方 Yahoo 知恵袋

1

タイルばり問題への鮮やかな証明 数学って面白い

数学を愛する会 V Twitter へぇ

最小公倍数と最大公約数で タイル敷き詰め と 素数ゼミ 問題を解く 数学ia Himokuri

最新 ブログ 数学月間の会sgk

数学ia Himokuri

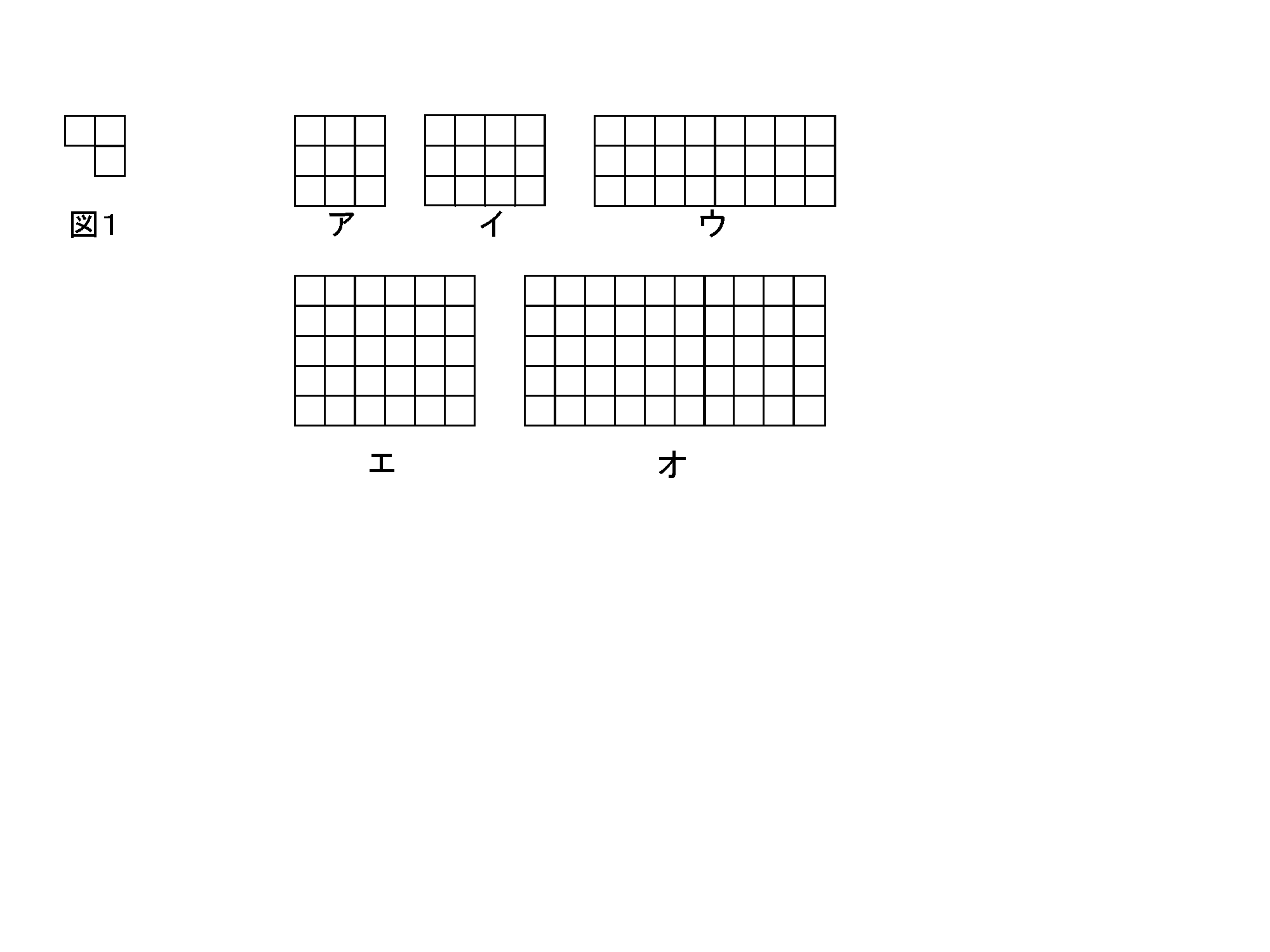
Tg Web 従来型 タイルの敷き詰めトレーニング問題

30年ぶり新5角形発見 難問タイル敷き詰め問題に新たな答え スクラップブック

10 10に1 4のタイルを敷き詰められますか 頭が柔らかくないと解けない算数 数学 4 Youtube

麻布中の算数入試問題 大問６ 東久留米 学習塾 塾長ブログ

タイル張り 数学屋ノート Note

受付カウンターにタイルを敷き詰めてみました すずろーぐ

2

1

この部屋に畳を敷詰められるか 頭が柔らかくないと解けない数学 2 Youtube

ワンのタイル Wikipedia

1種類のタイルによる敷き詰め変奏曲 第6 28回日曜数学会 ニコニコ動画

ワンのタイル Wikipedia

タイル敷き詰め問題がわかりません 8 8の盤面から 4つある角の Yahoo 知恵袋

幾何学的確率 コインを投げて決められた図形の中に収まる確率の出し方 たぬぬ塾 中学校の先生たち

小特集 4 個と群 アート サイエンス協働教育

3

数学クイズ パズル 面白い数学クイズ パズル 難問編 数学の面白いこと 役に立つことをまとめたサイト

敷き詰めの探究 Part 1 数理女子

正方形と最大公約数の関係について 横18cm縦24cmの長方 Yahoo 知恵袋

１マス欠損正方形敷き詰め問題 Takapの数学日記

ペンローズタイルの作り方 幾何学模様のブログ みずすましの図工ノート

Incoming Term: タイル 敷き詰め 数学,